Dokładność i rozdzielczość obrazowania termicznego
Większość przemysłowych kamer termowizyjnych wykorzystuje niechłodzone mikrobolometry do pomiaru temperatury obiektów lub wizualizacji odległych celów. Bardziej wydajne metody produkcji, w szczególności próżniowe pakowanie na poziomie wafli w przypadku powszechnie stosowanych cienkowarstwowych bolometrów, znacznie obniżyły koszty produkcji detektorów bolometrycznych. Te redukcje kosztów przyczyniły się do skalowania i penetracji czujników podczerwieni w różnych zastosowaniach przemysłowych do stacjonarnego, bezkontaktowego pomiaru temperatury. Zastosowania te obejmują zarówno badania przesiewowe w kierunku gorączki, jak i systemy kontroli jakości w produkcji, a także systemy wczesnego wykrywania pożaru. Biorąc pod uwagę, że powierzchnia czynna determinuje liczbę urządzeń, które można zmieścić na pojedynczym waflu krzemowym, a koszt produkcji całego wafla pozostaje względnie stały, niezależnie od liczby urządzeń, staje się oczywiste, że powierzchnia czynna ma decydujący wpływ na koszt jednostkowy urządzenia. Dlatego też, od ponad dwóch dekad, konsekwentne dążenie do mniejszych odstępów między detektorami jest trwającym trendem w technologii bolometrycznej. Znaczący postęp w rozwoju technologii produkcji czujników mikrobolometrycznych oraz jakość materiałów napędzały rynek detektorów podczerwieni, co doprowadziło do wzrostu gęstości pikseli detektorów z 2,72 mm x 2,72 mm dla detektora z rastrem pikseli 34 µm i rozdzielczości 80×80 do 3,84 mm x 2,88 mm dla detektora z rastrem pikseli 12 µm i rozdzielczości 320×240. Przekłada się to na mniejsze detektory i większą gęstość upakowania w mikroobróbce płytek półprzewodnikowych oraz ich przewagę cenową w porównaniu z detektorami o konwencjonalnych rozmiarach.
Niemniej jednak rozmiar piksela ma kluczowe znaczenie dla określenia charakterystyki osiągów urządzenia. Obserwowany trend w rozmiarach pikseli sugeruje, że wzrost liczby pikseli i zmniejszenie rozstawu pikseli budzi obawy dotyczące efektywnej powierzchni absorpcji detektora, co z kolei wpływa na ogólne osiągi urządzenia. Wraz z przechodzeniem branży na mniejsze rozstawy pikseli, konieczne są działania mające na celu zwiększenie czułości detektora, aby jednocześnie utrzymać jakość obrazowania. Opracowano innowacyjne struktury wielowarstwowe, absorbery i innowacyjne kombinacje materiałów. Kolejnym, głównym celem jest zmniejszenie wymiarów i kosztów związanych z niechłodzonymi bolometrami, a także zmniejszenie rozmiaru i kosztów zespołu soczewek. Obecnie koszty zespołu detektora i soczewki są zbliżone, co sprawia, że koszt soczewki ma istotny wpływ na cenę systemu. Poza kwestiami związanymi z pikselami, nieodłączna natura optyki, polegająca na przekształcaniu promieni podczerwonych w dyfrakcyjny wzór o zwiewnym kształcie, manifestowany przez funkcję rozproszenia punktowego, odgrywa kluczową rolę w ogólnej wydajności urządzeń do obrazowania w podczerwieni. Granica rozdzielczości Abbego, szczególnie w zastosowaniach mikroskopowych, stanowi wyzwanie dla niezależnego rozdzielania i rozróżniania szczegółów miniaturowych obiektów w podczerwieni.
Te wyzwania optyczne i związane z detektorem mają fundamentalny wpływ na zdolność kamery do uzyskania powtarzalnych wyników pomiaru temperatury, niezależnie od rozmiaru lub odległości od obiektu. Niniejsza publikacja przedstawia kontekst teoretyczny i wyniki eksperymentalne, które pozwalają odpowiedzieć na pytanie, czy wynik pomiaru temperatury pojedynczego piksela jest wiarygodny.
Jak optyka i detektor definiują rozdzielczość obrazowania termicznego
W niechłodzonej kamerze termowizyjnej opartej na bolometrze amplituda promieniowania podczerwonego jest precyzyjnie mierzona w celu uchwycenia i zobrazowania emisji cieplnych. Elementy detektora zmieniają swoją rezystancję z powodu absorpcji światła emitowanego w podczerwieni, co powoduje zmianę napięcia wyjściowego. W przypadku radiometrycznych pomiarów termograficznych, migawki mechaniczne są niezbędne do kompensacji przesunięcia w matrycach płaszczyzny ogniskowej, co jest wymagane przez fundamentalną zasadę bolometrycznych mostków rezystancyjnych i ich ograniczoną stabilność obwodów odczytu. Odstęp pikseli bolometru, czyli odległość między środkami pikseli, wpływa na rozdzielczość, czułość termiczną i jakość obrazu. Rozdzielczość obrazu to liczba pikseli w pionie i poziomie. Rozmiar piksela bezpośrednio wpływa na jego czułość. W tym przypadku większy raster pikseli daje z natury wyższą czułość ze względu na większą powierzchnię, przy tych samych właściwościach materiału.
Najważniejszą cechą wpływającą na rozdzielczość termiczną urządzenia termowizyjnego jest parametr NETD (Noise Equivalent Temperature Difference) czujnika. NETD reprezentuje najmniejszą różnicę temperatur, jaką czujnik może określić. Parametr ten odpowiada stosunkowi sygnału do szumu równemu jedności. Innymi słowy, zmiana sygnału wyjściowego czujnika przy różnicy temperatur równej NETD odpowiada poziomowi szumu czujnika. Im niższa wartość NETD, tym wyższa czułość czujnika. Oprócz wydajności detektora, parametry optyczne układu optycznego determinują jakość obrazu, kontrast i rozdzielczość całego systemu. Wrodzona właściwość układu optycznego, polegająca na przekształcaniu promieni podczerwonych w dyfrakcyjny wzór o zwiewnym kształcie, manifestowany przez funkcję rozproszenia punktowego, odgrywa kluczową rolę w ogólnej wydajności urządzeń do obrazowania w podczerwieni. Gdy promienie światła emitowane z obiektu wchodzą do układu optycznego, dyfrakcja zachodzi na styku urządzenia optycznego z jego otoczeniem.
Dlatego odległy punkt świetlny nie jest obrazowany jako pojedynczy punkt, lecz jako plamka Airy'ego otoczona kilkoma wąskimi, koncentrycznymi okręgami o malejącej intensywności w kierunku zewnętrznym. Każda soczewka ma określoną górną granicę wydajności, znaną jako granica dyfrakcyjna. Granica ta jest teoretyczną maksymalną zdolnością rozdzielczą soczewki. Rozpatrując układ soczewek, zakłada się, że płaszczyzna obiektu jest macierzą niespójnych źródeł punktowych. Jeśli źródła punktowe są niespójne, płaszczyzna obrazu składa się z niezależnych plamek Airy'ego nałożonych na siebie. Zgodnie z kryterium Rayleigha, dwa obiekty są rozróżnialne, jeśli maksymalna jasność jednego obiektu pokrywa się z pierwszą minimalną jasnością drugiego obiektu. Granica rozdzielczości Δlmin, przy której dwa piksele mogą być nadal rejestrowane jako oddzielne, to granica rozdzielczości Δlmin, przy której λ to użyta długość fali, f to ogniskowa, a D to średnica soczewki.
\[r = \Delta l_{min} = 1,22 \frac {f \lambda}{D}\]
To równanie opisuje również promień r plamki Airy'ego. Rozdzielczość optyczną układu optycznego definiuje się zazwyczaj jako odwrotność wspomnianego równania 1/Δlmin. Rysunek 1 przedstawia układ soczewek i bolometr w sposób poglądowy. W tym przypadku plamka Airy'ego jest najmniejszym punktem, na którym można skupić wiązkę światła. Ze względu na ograniczenia dyfrakcyjne, najmniejszy punkt, na którym można skupić wiązkę światła, jest ograniczony.
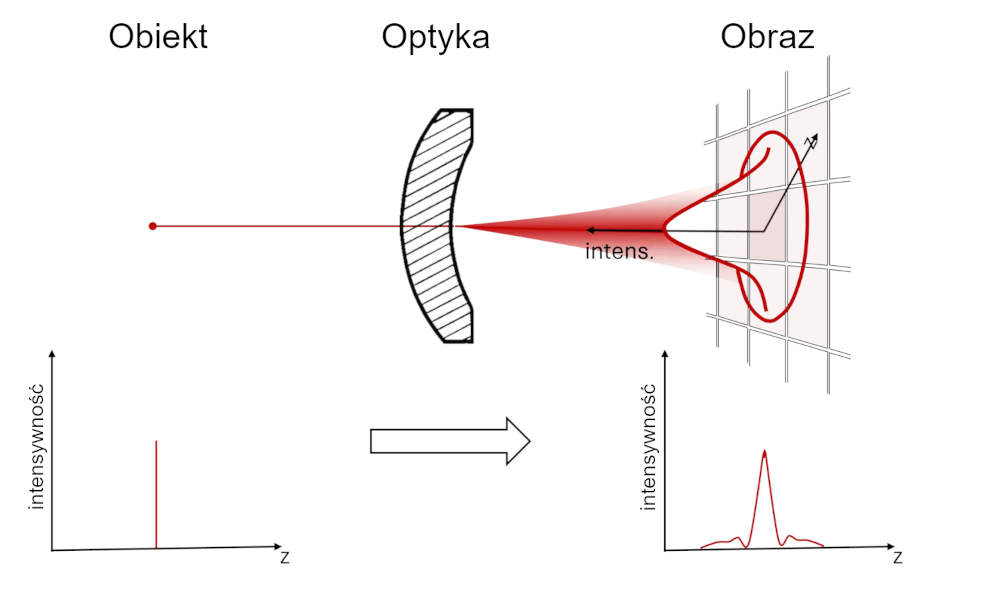
Rysunek 1. Gdy światło przechodzi przez dowolną aperturę lub soczewkę o dowolnym rozmiarze, następuje dyfrakcja, a natężenie plamki Airy'ego oświetla piksel bolometru. Dysk Airy'ego jest najmniejszym punktem, na którym można skupić wiązkę światła. Średnica tego wzoru jest związana z długością fali i rozmiarem apertury. Aby zmierzyć całkowitą energię promieniowania podczerwonego, cały wzór musi zostać pobrany przez wszystkie pokryte piksele.
W miarę jak średnica D zbliża się do długości fali, plamki Airy'ego stają się bardzo duże, a apertura coraz bardziej przypomina otwór szpilkowy. Jeśli rozdzielczość wymaga poprawy, można na przykład pracować z krótszymi falami. Im mniejsza długość fali i większa średnica soczewki, tym większa rozdzielczość. Niemniej jednak, w każdym układzie soczewek o pomijalnych aberracjach, dyfrakcyjna ekspansja poszczególnych pikseli wyznacza nieprzekraczalną granicę jakości obrazu.
Rysunek 2 ilustruje, że mniejsze odstępy między pikselami i mniejsza optyka powodują rozproszenie dysku Airy'ego ze względu na ograniczenie dyfrakcyjne, które musi zostać pobrane przez jeszcze większą liczbę pikseli.
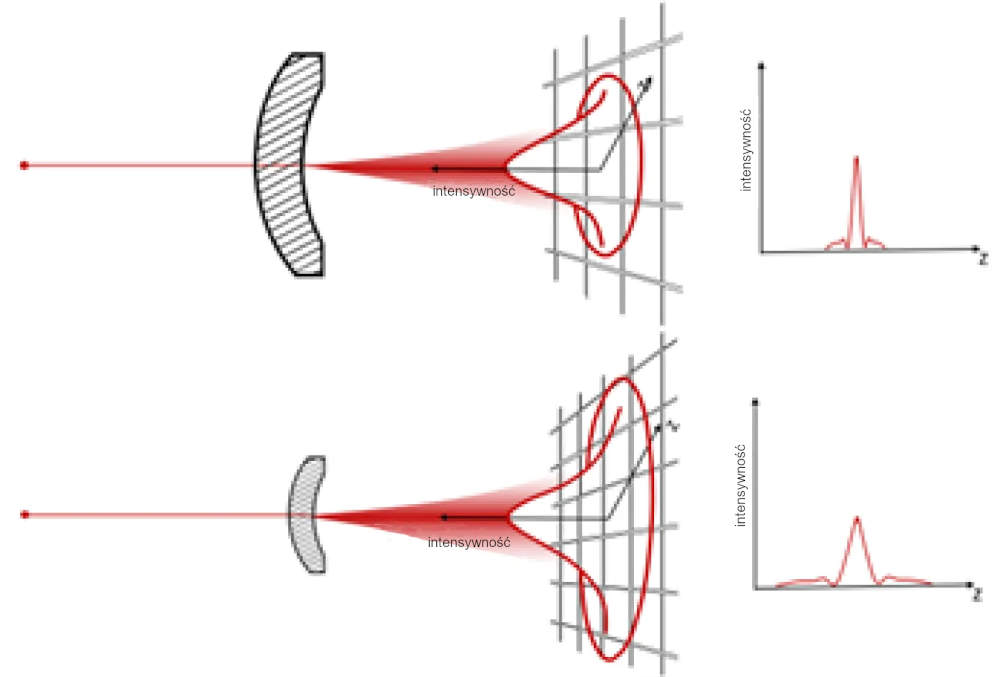
Rysunek 2. Rozważając układ o mniejszym odstępie między pikselami w połączeniu z mniejszym układem soczewek, dysk Airy'ego staje się fundamentalnym wyzwaniem. Wraz ze zmniejszaniem się średnicy soczewki, wraz ze wzrostem dyfrakcji, plamka Airy'ego staje się szersza i obejmuje więcej pikseli. Aby uzyskać precyzyjny pomiar natężenia promieniowania podczerwonego, należy zmierzyć całą funkcję Airy'ego.
Rysunek 3 ilustruje widok z góry na bolometr o innym rastrze. Przyjęto tu podobną optykę. Ze względu na ograniczenie dyfrakcyjne optyki, plamka Airy'ego ma tę samą szerokość. Aby zmierzyć całkowitą moc padającego światła podczerwonego, konieczne jest pobranie próbek większej liczby pikseli. Co więcej, teoria pomija potencjalne ograniczenia w konstrukcji soczewek i błędy produkcyjne nieodłącznie związane z wytwarzaniem elementów soczewek lub układów optycznych. Czynniki te ograniczają uzyskanie najmniejszego fizycznie osiągalnego punktu, co w konsekwencji obniża poziom rozdzielczości i kontrastu.
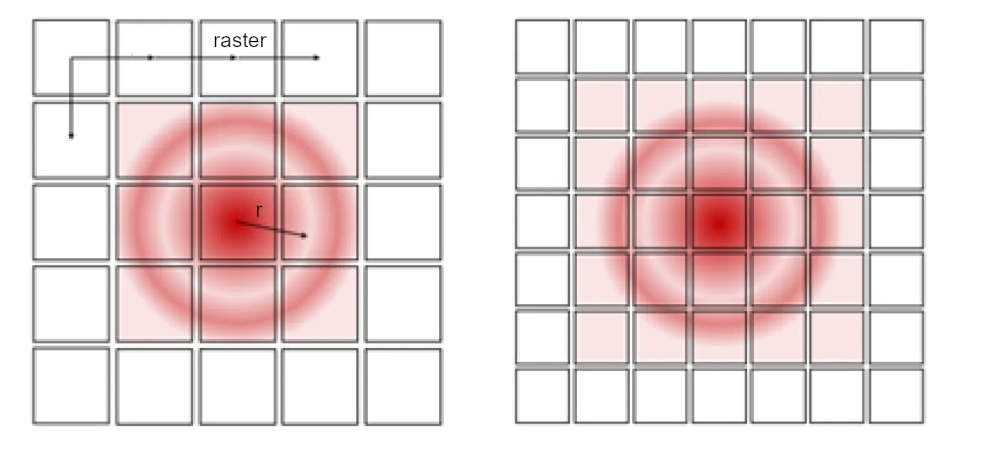
Rysunek 3. Biorąc pod uwagę układ o mniejszym skoku pikseli i podobnej optyce, powstała plamka Airy'ego obejmuje więcej pikseli. Wszystkie oświetlone piksele muszą zostać pobrane próbek w celu dokładnego pomiaru natężenia, co zilustrowano tutaj jasnoczerwonym kolorem. Nawet w systemach czujnikowych z drobniejszymi pikselami jakość obrazu nie poprawia się ze względu na ograniczenia dyfrakcyjne.
Do tej pory rozważano tylko jedno źródło światła podczerwonego. Zakładając, że skupione wzory Airy'ego z różnych obiektów zbliżają się do siebie, wzory nakładają się na siebie. Wzory ostatecznie stają się nieodróżnialne, jeśli nakładające się wzory powodują wystarczającą interferencję, aby zmniejszyć kontrast. Ponieważ najmniejszy osiągalny rozmiar plamki przekracza rozmiar małych pikseli nowoczesnych bolometrów długofalowych, uzyskanie pełnej rozdzielczości i wysokiego poziomu kontrastu staje się coraz trudniejsze. Najmniejsza możliwa do rozróżnienia odległość kątowa, poniżej której obiekt nadal może być postrzegany jako oddzielny, to odległość, w której pierwsze minimum dyfrakcyjne przypada na szczyt drugiej plamki Airy'ego. Odległość w polu widzenia obrazu między punktami na obrazie nazywana jest granicą rozdzielczości. Dlatego rozproszenie ograniczone dyfrakcją jest aproksymowane średnicą pierwszego zera plamki Airy'ego.
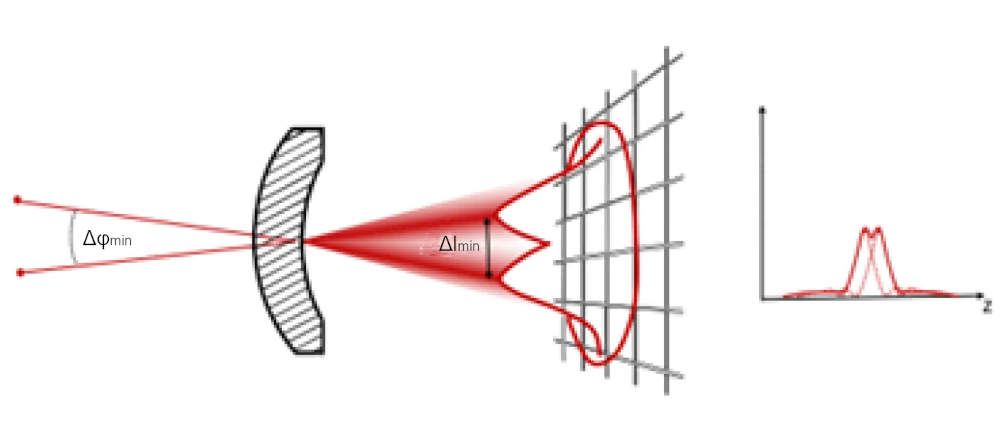
Rysunek 4. Nałożone obrazy dyfrakcyjne na bolometrze. Najmniejsza możliwa do rozróżnienia odległość kątowa, poniżej której obiekt może być nadal postrzegany jako oddzielny, to odległość, w której pierwsze minimum dyfrakcyjne przypada na szczyt drugiej plamki Airy'ego. Odległość między punktami na obrazie nazywana jest granicą rozdzielczości.
Szczególnie w zastosowaniach mikroskopowych częściej odwołuje się do granicy rozdzielczości Abbego. W tym przypadku definicja Abbego jest bardzo zbliżona do przedstawionego równania, ale uwzględnia aperturę numeryczną NA zamiast liczby f, co skutkuje najmniejszym rozmiarem obiektu możliwego do rozróżnienia d. Apertura numeryczna (NA) układu mierzy kąty, pod którymi światło może wejść lub wyjść z układu. Oba te terminy są ze sobą powiązane. W przeciwieństwie do liczby f, apertura numeryczna uwzględnia współczynnik załamania n ośrodka, w którym układ pracuje.
\[d = \frac {\lambda }{2n \times sin ( \varphi )} = \frac{\lambda }{2NA}\]
Z tych rozważań wywodzą się terminy pole widzenia pomiaru MFOV i chwilowe pole widzenia IFOV. Podczas gdy chwilowe pole widzenia definiuje rozmiar pojedynczego piksela na powierzchni pomiarowej, termin pole widzenia pomiaru opisuje zalecany minimalny rozmiar obiektu dla powtarzalnego i dokładnego pomiaru. Oba te terminy są obliczane na podstawie rozmiaru piksela, odległości od obiektu pomiarowego oraz pionowego i poziomego pola widzenia układu optycznego.
Analiza porównawcza osiągów bolometrów 12 µm, 17 µm i 34 µm
W dalszej części porównano trzy różne kamery termowizyjne o różnych odstępach pikseli. W tym celu wykorzystano porównywalne układy optyczne, aby podkreślić właściwości detektora. Raster pikseli wynosi 34 µm, 17 µm i 12 µm. Liczba F układu optycznego kamery jest bliska 1. Tabela 1 porównuje kamery ze sobą.
| Raster [µm] | 12 | 17 | 34 |
| Rozmiar detektora [mm] | 7.68 x 5.76 | 10.88 x 8.16 | 2.72 x 2.72 |
| NETD [mK] | 60 | 40 | 100 |
| Rozdzielczość [px] | 640×480 | 640×480 | 80×80 |
| Ogniskowa f [mm] | 13 | 19 | 5 |
| Jasność obiektywu (F) | 0.9 | 0.8 | 0.9 |
| Kąty widzenia (FOV) | 36° x 26° | 33° x 25° | 30° x 30° |
| Częstotliwość ramki [Hz] | 32 | 32 | 50 |
Tabela 1. Przegląd parametrów kamery termowizyjnej.
W tym eksperymencie bada się wielkość energii w okręgu. Oblicza się ją, wstępnie oceniając całkowitą energię na płaszczyźnie obrazu i porównując ją z energią wychwyconą przy mniejszych rozmiarach obrazu. W związku z tym matryca płaszczyzny ogniskowej jest oświetlana przez duże ciało doskonale czarne, aby zapewnić, że każdy piksel odbiera pełną intensywność, a skupiona płaszczyzna obrazu jest o wielkość liter większa niż rozmiar piksela. Dodatkowa apertura między kamerą a źródłem stałego promieniowania podczerwonego zmniejsza rozmiar obrazu. Rysunek 5 ilustruje eksperyment z wykorzystaniem źródła światła w postaci ciała doskonale czarnego ustawionego na 100°C. Przed ciałem doskonale czarnym zamontowano aperturę o zmiennej średnicy. Pojedynczy piksel w centrum otrzymuje maksymalną energię, jeśli apertura jest wystarczająco duża, aby nie zaburzać drogi optycznej. Dzięki zmniejszeniu promienia, obejmuje mniej energii. Pojedynczy piksel w centrum otrzymuje mniej energii wraz ze zmniejszaniem się rozmiaru obrazu, a funkcja rozproszenia punktowego rozprzestrzenia się na wiele pikseli matrycy płaszczyzny ogniskowej z powodu dyfrakcji. Energia w okręgu porównuje wychwyconą intensywność i odnosi ją do całkowitej mocy. Zatem rozciąga się od zera do jedności, ponieważ jest znormalizowane do całkowitego natężenia energii.

Rysunek 5. Ciało doskonale czarne o zmiennej aperturze jest używane do stworzenia obiektu o małym rozmiarze. Kamera monitoruje te obiekty za pomocą pikseli o różnym rastrze. Dlatego dla uproszczenia ocenia się reakcję temperaturową pojedynczej linii na matrycy FPA.
Konwencjonalnie w pirometrii stosunek odległości do rozmiaru plamki to średnica ciała doskonale czarnego, przy której sygnał promieniowania zmniejszył się o 10% w porównaniu z sygnałem wystarczająco dużego ciała doskonale czarnego. Definicja ta uwzględnia aberracje sferyczne i chromatyczne układu optycznego, efektywną powierzchnię detektora oraz efekty rozpraszania w układzie optycznym. Wywodząc się z tej definicji dla pirometrów, rozmiar obrazu przy 90% energii w okręgu definiuje pole widzenia kamery termowizyjnej. W rezultacie rozmiar obrazu i 90% energii w okręgu są również powiązane z liczbą pikseli wymaganych do pokrycia obrazu zogniskowanego. W przypadku obrazów o mniejszych rozmiarach, energia otoczona maleje w stosunku do rzeczywistej energii całkowitej pojedynczego piksela tak bardzo, że metody pomiaru oparte na intensywności, takie jak konwencjonalne systemy kamer termozicynych, generują zbyt małą wartość temperatury.
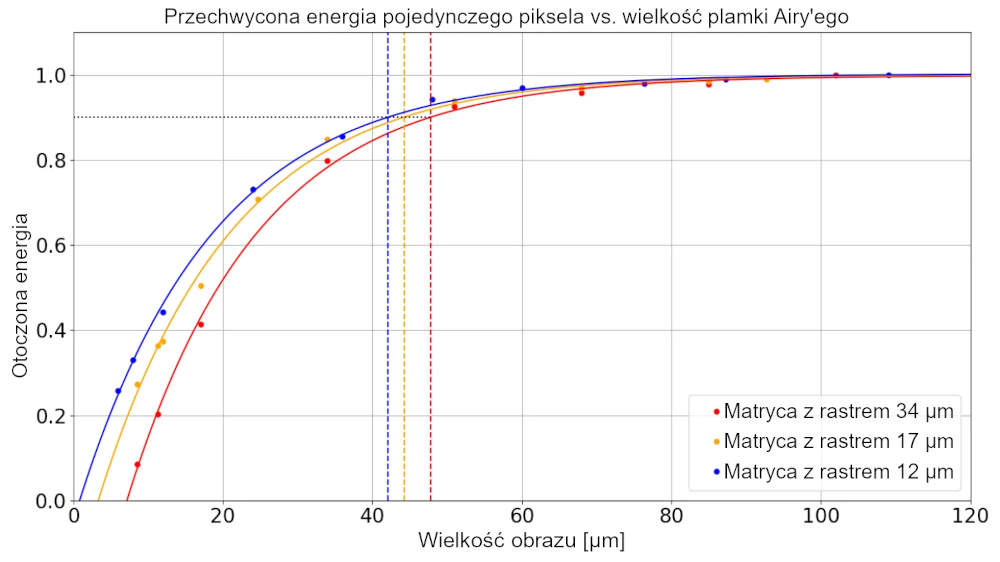
Rysunek 6. Otoczona energia w odniesieniu do rozmiaru obrazu skupionego na matrycy FPA. Wraz ze zmniejszającą się aperturą, pojedynczy piksel nie otrzymuje już całkowitej energii. Pojedynczy piksel w centrum otrzymuje mniej energii wraz ze zmniejszaniem się rozmiaru obrazu, a funkcja rozproszenia punktu rozprzestrzenia się na wiele pikseli matrycy płaszczyzny ogniskowej ze względu na limit dyfrakcyjny, który jest wyświetlany jako czarna linia.
Rysunek 6 ilustruje eksperyment na wykresie. Rozmiar obrazu przy 90% energii w okręgu jest również zaznaczony w Tabeli 2.
| Raster [µm] | Rozmiar obrazu przy 90% energii otoczonej [µm] |
Liczba pikseli wymagana do dokładnego pomiaru |
| 34 | 47.85 | 2 |
| 17 | 44.24 | 3 |
| 12 | 42.08 | 4 |
Tabela 2. Rozmiar obrazu przy 90% energii otoczonej w porównaniu dla różnych podziałek pikseli. To podsumowanie pokazuje, że w przypadku kamer na podczerwień z małymi podziałkami matryc płaszczyzny ogniskowej należy uwzględnić więcej pikseli, aby zapewnić dokładne pomiary intensywności lub temperatury.
Przy temperaturze ciała czarnego 100°C, zmiana wykrytej energii o ~10% odpowiada odchyleniu temperatury o 7,2°C. Rysunki 7 i 8 ilustrują wyniki w dziedzinie temperatury. W tym przypadku wykorzystano skanowanie liniowe w poprzek źródła punktowego. Na rysunku 7 źródło punktowe zostało zmniejszone do rozmiaru, tak aby oświetlony był tylko jeden piksel. Dla każdej kamery o różnych podziałkach pikseli wprowadzono odchylenie pomiaru. Odchylenie pomiaru jest największe dla kamery o najmniejszym odstępie pikseli. Na rysunku 8 rozmiar obiektu został zwiększony do minimalnego zakresu optycznego. Chociaż możliwe jest wykrycie cech obiektu o mniejszej skali, minimalny rozmiar obiektu lub średnica źródła punktowego na obrazie jest większa ze względu na jego optyczny, podczerwony charakter, a nie rozdzielczość pikseli.
Podsumowując, aby dokładnie zmierzyć mały obiekt, musi on obejmować co najmniej 2×2 piksele przy rastrze 34 µm, 3×3 px przy rastrze 17 µm i 4×4 px [rzy rastrze 12 µm.
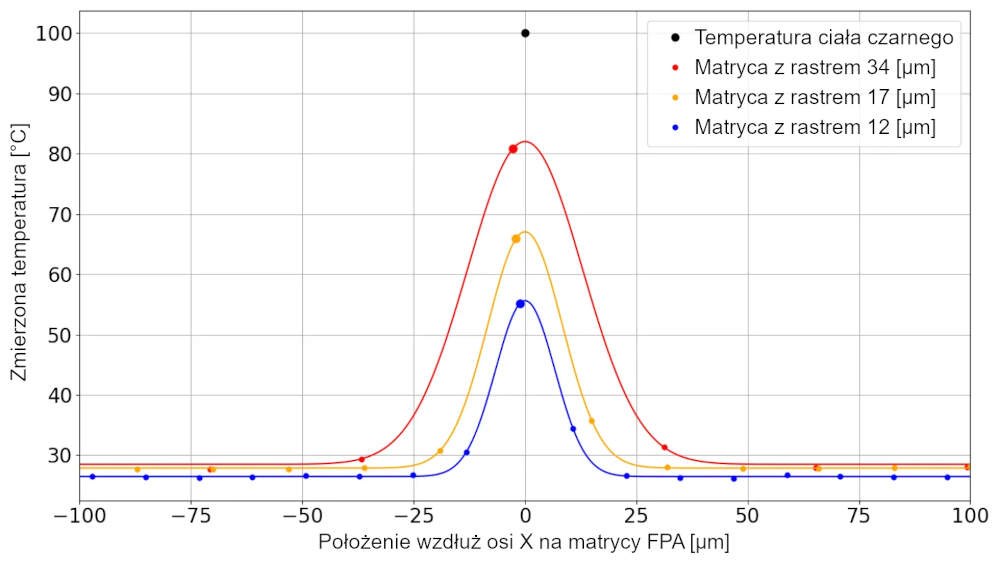
Rysunek 7. Wyniki pomiaru temperatury dla skanowania liniowego źródła punktowego. Źródło punktowe ma niewielki rozmiar, więc oświetlany jest tylko jeden piksel na bolometrze. Ze względu na różnice w odstępach pikseli, kamera o odstępie pikseli 12 µm ma największe odchylenie pomiaru. Aby uzyskać dokładny pomiar temperatury, rozmiar obiektu musi być większy.
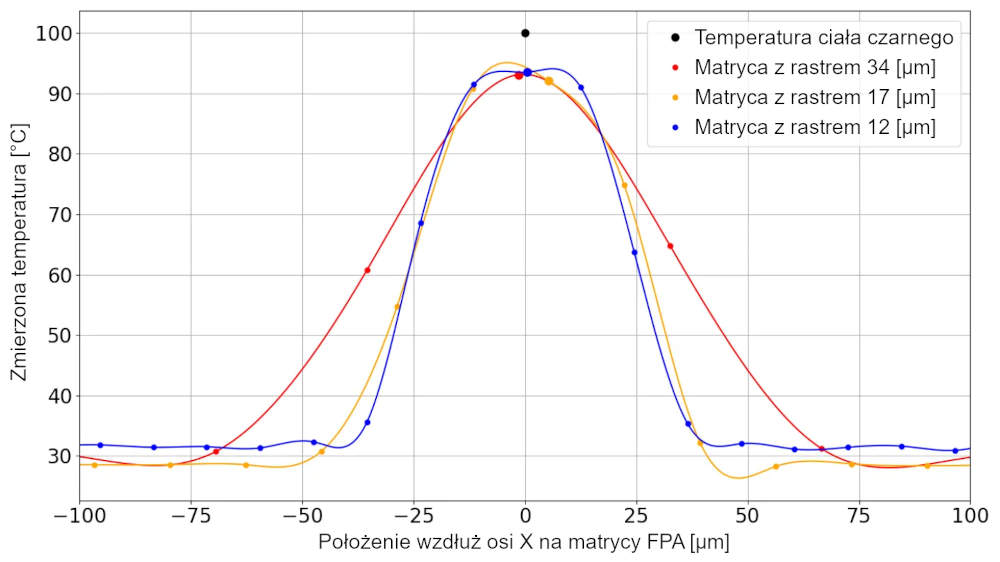
Rysunek 8. Wyniki pomiaru temperatury dla skanowania liniowego źródła punktowego, odpowiadającego polu widzenia pomiaru, są ograniczone ze względu na jego naturę optyczną. Aby dokładnie zmierzyć ten obiekt, należy rozważyć zastosowanie rozdzielczości 2×2 dla rozdzielczości pikseli 34 µm, 3×3 dla rozdzielczości pikseli 17 µm i 4×4 pikseli dla rozdzielczości pikseli 12 µm.
Wydajność pomiaru różni się znacząco w realistycznym zastosowaniu, w którym obiekt pomiarowy znajduje się 1 m od kamer i ma porównywalną optykę, co skutkuje podobnym polem widzenia. Chociaż chwilowe pole widzenia wynosi 0,94 mm (mrad) w odległości 1 m, kamera wskazywałaby różne temperatury obiektu o rozmiarze IFOV. Tabela 3 podsumowuje wyniki tego eksperymentu. Pomijając koszty, w tym przykładowym zastosowaniu kamera o rozdzielczości pikseli 17 µm jest najlepszym rozwiązaniem, ponieważ pole widzenia pomiaru jest najmniejsze.
| Raster [µm] | IFOV [mm] 1x1 px |
Błąd pomiaru [°C] IFOV |
MFOV [mm] [N x N] px |
Błąd pomiaru [°C] MFOV |
| 34 | 6.97 | -20 | 13.9 [2×2] | -7 |
| 17 | 0.94 | -33 | 2.82 [3×3] | -5 |
| 12 | 0.98 | -45 | 3.91 [4×4] | -6 |
Tabela 3. Wyniki pomiarów kamery o różnym rastrze pikseli.
Postęp w wydajności bolometrów umożliwia nowe zastosowania, zwłaszcza tam, gdzie małe punkty pomiarowe muszą być elastycznie rozmieszczane i charakteryzować się niskim kontrastem termicznym na dużych odległościach. Koszt kamery będzie miał silny wpływ na jej przyjęcie, ale utrzymanie czułości staje się trudniejsze wraz ze wzrostem gęstości pikseli na płytkach. Granice dyfrakcji optycznej pozostają fundamentalnym ograniczeniem rozdzielczości i jakości obrazu, nawet gdy rozmiary pikseli zbliżają się do długości fali detekcji. Chociaż cyfrowe wzmocnienie kontrastu może poprawić wygląd wizualny, może zwiększyć szum i nie przezwycięża ograniczeń fizycznych. W termowizji długofalowej odczyty temperatury z pojedynczego piksela są mało wiarygodne, ponieważ dysk Airy'ego indukowany dyfrakcją przekracza rozmiar piksela, zmniejszając energię otaczającą i dokładność pomiaru.
Podsumowanie
- Mniejszy raster pikseli w bolometrach zmniejsza koszty i zwiększa rozdzielczość, ale może obniżyć czułość i wymagać większej liczby pikseli do dokładnego pomiaru temperatury ze względu na ograniczenia dyfrakcyjne.
- Dyfrakcja optyczna (plamka Airy'ego) nakłada sztywne ograniczenia na rozdzielczość, przez co odczyty temperatury z pojedynczego piksela są mało wiarygodne, szczególnie w przypadku fal o dużej długości.
- Dokładne pomiary wymagają, aby mierzony obiekt obejmował wiele pikseli (np. 4×4 piksele przy rastrze 12 µm), aby uchwycić wystarczającą ilość energii otaczającej.
- Koszt i osiągi obiektywu odgrywają równie ważną rolę, co konstrukcja detektora, w ogólnej jakości obrazu i dokładności pomiaru.
- Raster pikseli 17 µm zapewnia dobry kompromis między czułością, rozdzielczością i wiarygodnym polem widzenia pomiaru w testowanych warunkach.
Źródła
- A. Rogalski: History of infrared detectors, Opto−Electronics Review 20(3), 279–308, DOI: 10.2478/s11772−012−0037−7
- P.V. Karthik Yadav, I. Yadav, B. Ajitha, A. Rajasekar, S. Gupta, Y. Ashok Kumar Reddy: Advancements of uncooled infrared microbolometer materials: A review, Volume 342, 2022, https://doi.org/10.1016/j.sna.2022.113611
- J. W. Franks, T. Hingant, P. Vervoort: The evolution of lens designs for 12micron uncooled LWIR detectors
- N. Schuster, J. Franks: Challenges, constraints and results of lens design in 8-12micron waveband for bolometer-FPAs having a pixel pitch of 12micron, Proc. SPIE, Vol. 8704-132 (2013)
- M. Guillaumont et al: Recent thermoresistive material evolutions at LYNRED for improving uncooled microbolometer products thermal sensitivity, Proc. SPIE 12107, Infrared Technology and Applications XLVIII, 1210716 (27 May 2022); https://doi.org/10.1117/12.2618494
- Lynred press release, Grenoble, France, November 17, 2021: Lynred boosts thermal sensitivity across range of 12-micron infrared detectors
- S. Cortial et al: Status of 8.5μm pitch bolometer developments at Lynred, Proc. SPIE 12534, Infrared Technology and Applications XLIX, 125341A (13 June 2023); https://doi.org/10.1117/12.2663455