Od prawa Plancka do Stefana-Boltzmanna
Prawo Stefana–Boltzmanna, zwane również prawem Stefana, definiuje całkowitą energię emitowaną na jednostkę powierzchni przez ciało doskonale czarne w stanie równowagi termicznej. Aby określić całkowitą moc promieniowania obiektu, należy pomnożyć jego powierzchnię A przez jego powierzchnię. Prawo wyraża wartość promieniowania M jako funkcję temperatury. Wartość promieniowania oznaczona kółkiem w indeksie górnym oznacza wartości charakterystyczne dla ciała doskonale czarnego.
\[M(T) = \varepsilon · M(T)= \varepsilon \times \sigma \times T^4\]
Stała proporcjonalności σ nazywana jest stałą Stefana–Boltzmanna σ i jest wyprowadzana z fundamentalnych stałych fizycznych.
\[\sigma = \frac {2 \pi^5 \times k_B^2}{15c^2 \times h^3} = 5670.10^{−8} Wm^{−2}K^{−4}\]
W ogólnym przypadku prawo Stefana–Boltzmanna dla promieniowania wyjściowego przyjmuje postać emisyjności powierzchni emitującej promieniowanie. W przypadku ciała szarego moc P emitowanego promieniowania dla obszaru A jest korygowana przez emisyjność ε, która uwzględnia zdolność materiału do emisji promieniowania podczerwonego.
\[P(T)=AM(T)=A \times \varepsilon \times \sigma \times T^4\]
Prawo można wyprowadzić, całkując prawo Plancka po widmie całkowitym i półsferze, uwzględniając prawo cosinusów Lamberta, gdzie Bλ(λ,T) to widmo radiancji z prawa Plancka, dΩ = sin(θ) dθ dϕ to element kąta bryłowego w sferycznych współrzędnych biegunowych, θ to kąt między normalną do powierzchni a kierunkiem promieniowania, ϕ to kąt kierunku w półprzestrzeni, a wyrażenie cos(θ) odpowiada prawu Lamberta.
\[M(\lambda ,T)=\int^\infty_0 \int B_\lambda (\lambda,T) cos(\sigma)d \Omega d \lambda\]
Ponieważ Bλ(λ,T) jest niezależne od kierunku, całka kątowa po półkuli upraszcza się do postaci, ponieważ całkowanie członów trygonometrycznych daje prosty czynnik π.
\[M°(λ,T)=\int^\infty_0 B_\lambda(\lambda,T) d \lambda \int^{\frac{π}{2}}_0 cos(\theta)sin(\theta)d \theta \int^{2 \pi}_0 d(\varphi)=\int^{\infty}_0 B_\lambda (\lambda ,T) d \lambda \times \frac {1}{2} \times 2 \pi\]
Całkowanie radiancji widmowej Bλ(λ,T) wymaga podstawienia składowej wykładniczej x=hcλ kB T tak, aby dλ=−hλ2 kB T dx, a po uwzględnieniu całki Bosego-Einsteina równanie upraszcza się do następującej postaci:
\[M°(\lambda ,T)=\pi \int^{\infty}_0 B_\lambda(\lambda ,T) d \lambda=2 \pi \times hc^2 {\frac {k_BT}{hc}}^4 \int^{\infty}_0 \frac {x^3}{e^−1}dx=2π \times hc^2 \frac {k_BT}{hc} \frac {\pi^4}{15}=\frac {2π^5k_B^4}{15 c^2 h^3}T^4\]
Ostatni człon reprezentuje wprowadzoną już stałą Stefana–Boltzmanna i dowodzi, że moc emitowana przez ciało doskonale czarne jest proporcjonalna do czwartej potęgi jego temperatury. Rysunek 1 ilustruje zależność między widmem emitowanego promieniowania a mocą emitowaną.
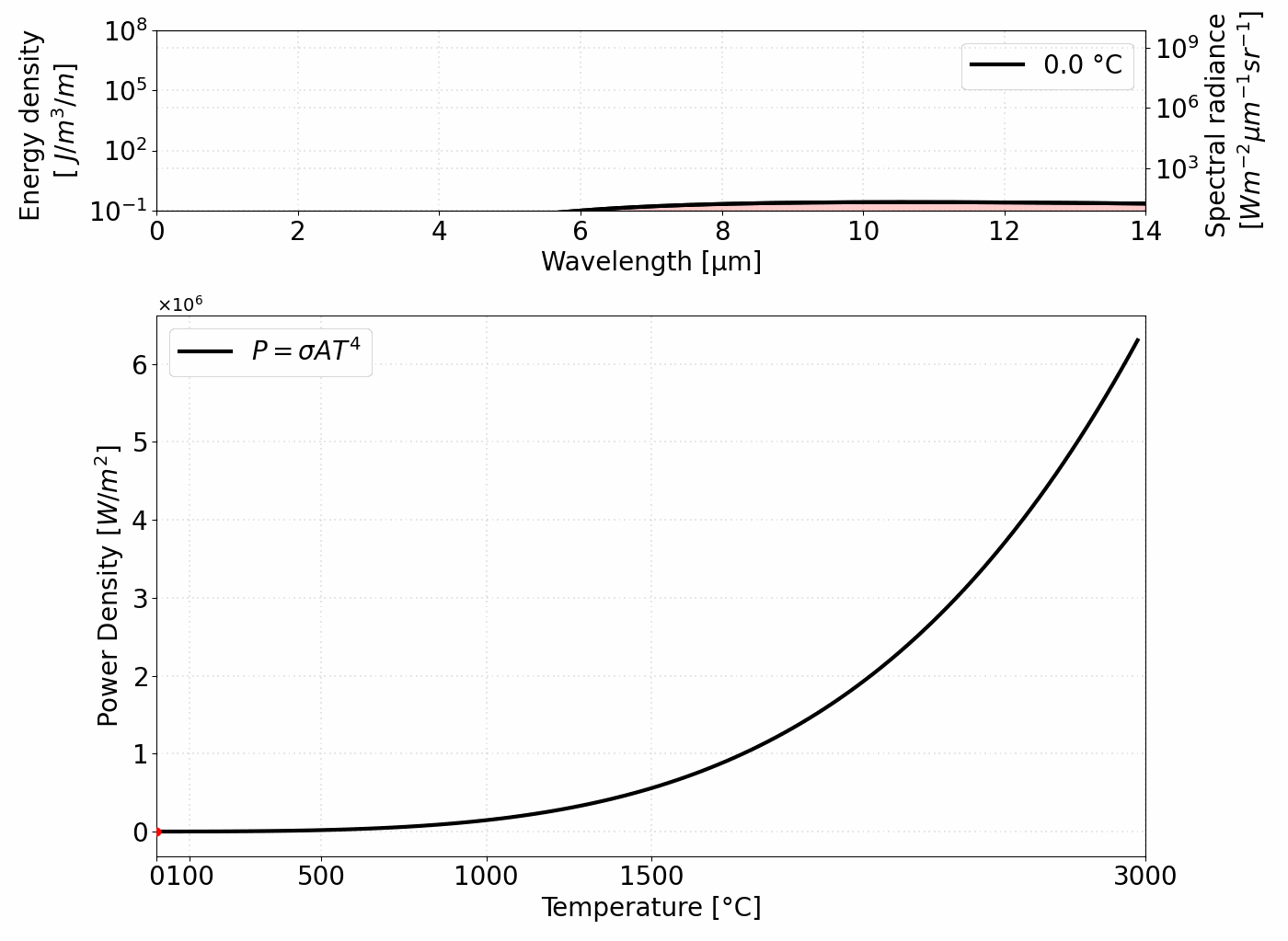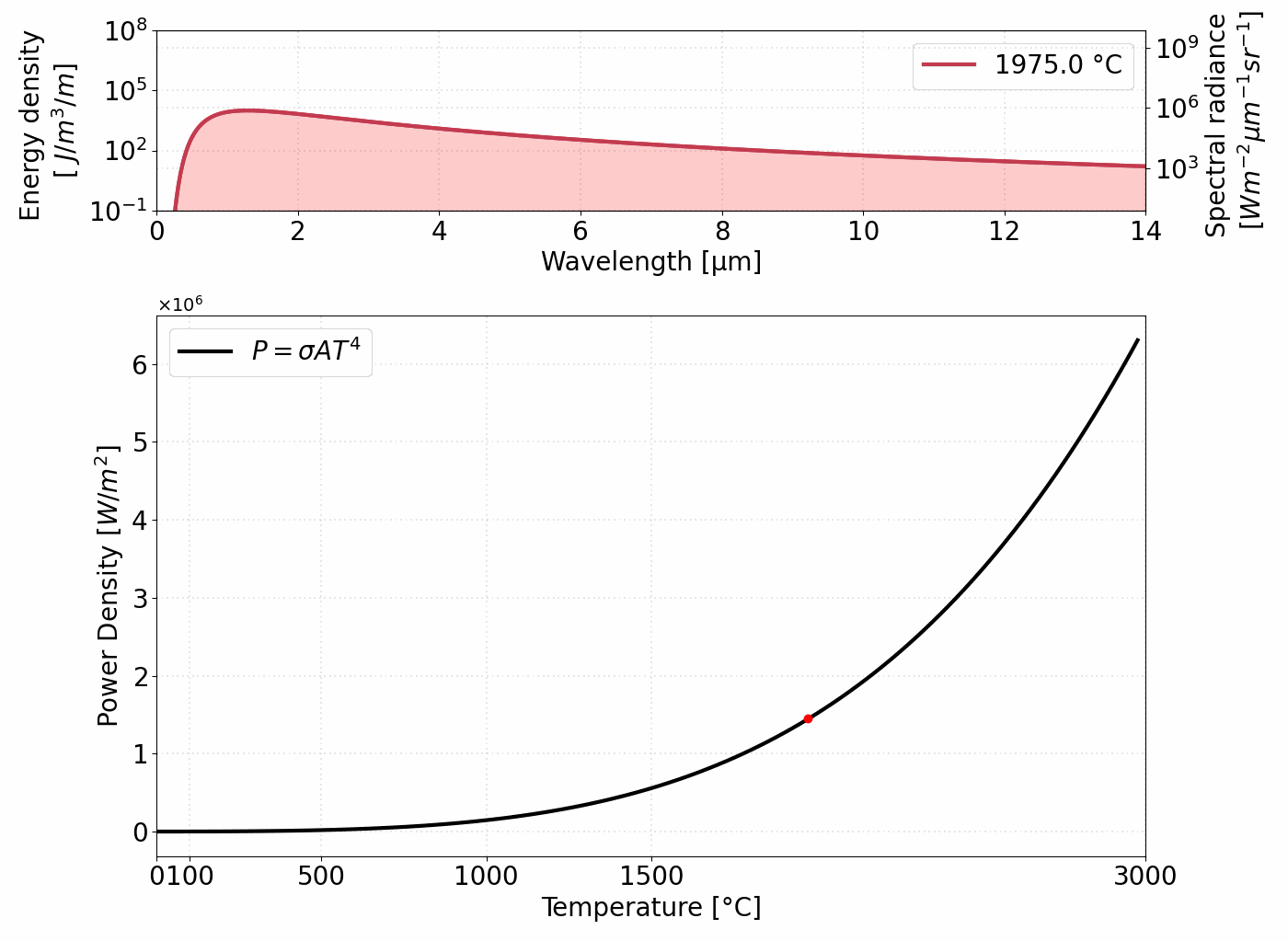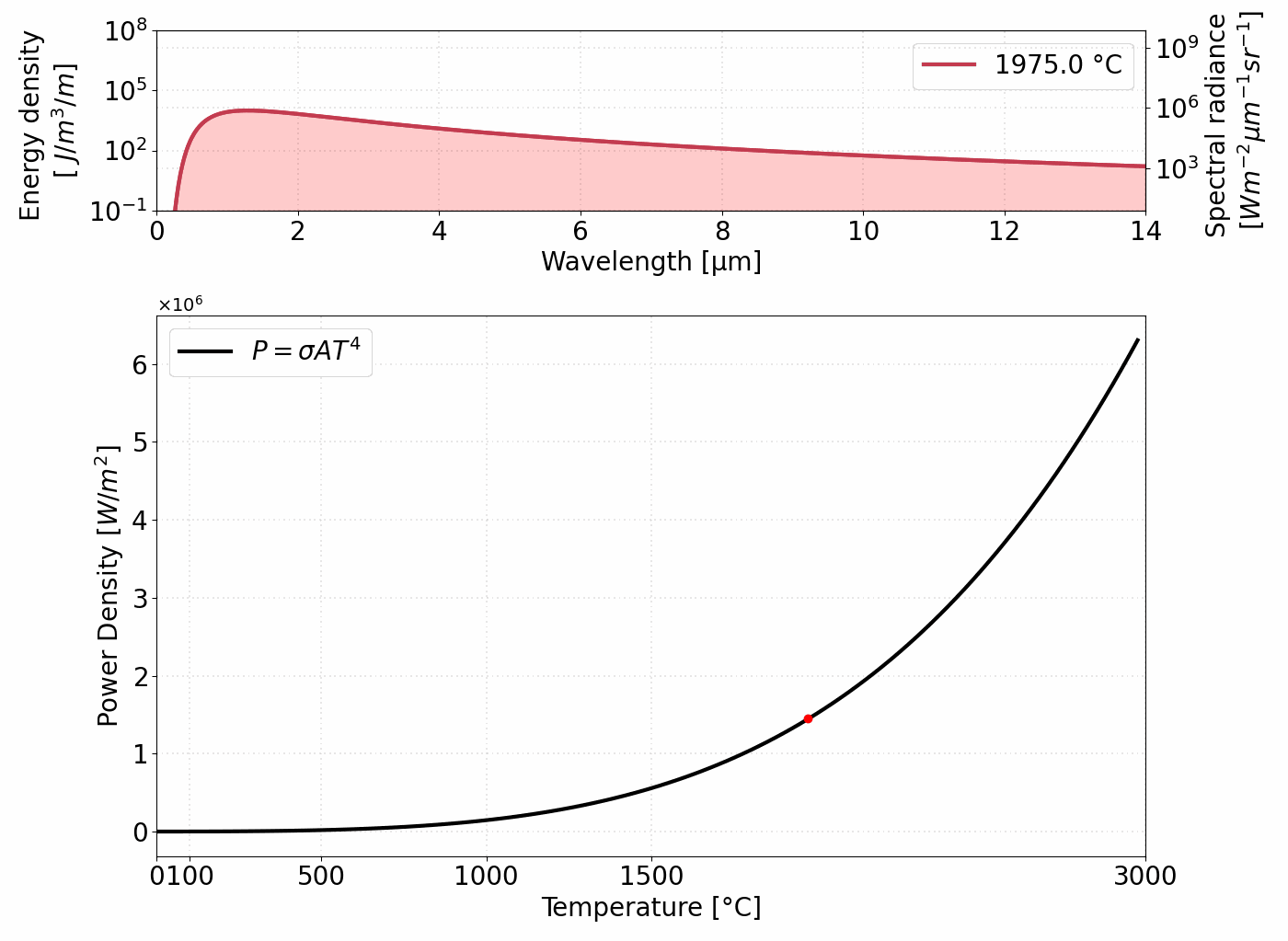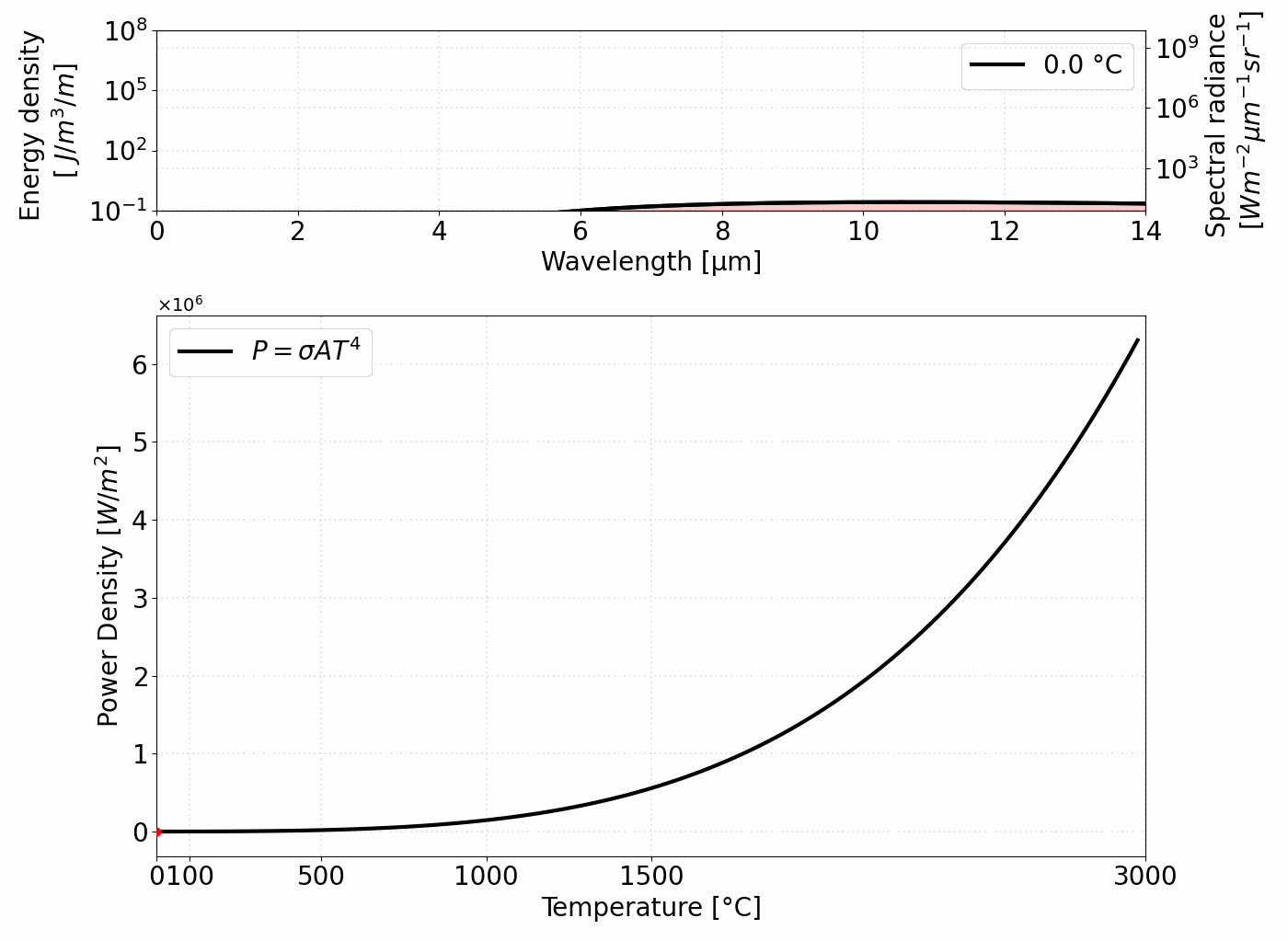
Całkowita moc (P) emitowana na jednostkę powierzchni ciała doskonale czarnego jest proporcjonalna do czwartej potęgi jego temperatury.
Podsumowanie
- Prawo Stefana–Boltzmanna głosi, że całkowita energia emitowana na jednostkę powierzchni przez ciało doskonale czarne jest proporcjonalna do czwartej potęgi jego temperatury.
- Prawo to wywodzi się z prawa promieniowania Plancka, przez zcałkowanie radiancji widmowej po wszystkich długościach fal i we wszystkich kierunkach, z uwzględnieniem prawa Lamberta.
Źródła
- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653
- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics rules of thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485
- De Witt, Nutter: Theory and Practice of Radiation Thermometry, 1988, John Wiley & Son, New York, https://doi.org/10.1002/9780470172575