Prawo Lamberta
Prawo Lamberta głosi, że promieniowanie z ciała doskonale czarnego w stanie równowagi termicznej jest emitowane równomiernie we wszystkich kierunkach, ale wydaje się słabsze pod kątem ze względu na efekty projekcji. Prawo to wskazuje, że obserwowane natężenie promieniowania z idealnego promiennika rozproszonego jest wprost proporcjonalne do cosinusa kąta między linią widzenia czujnika podczerwieni a normalną do powierzchni. Strumień promieniowania z małej powierzchni maleje wraz z kosinusem kąta emisji θ względem normalnej do powierzchni. Oznacza to, że maksymalne promieniowanie jest emitowane prostopadle do powierzchni (θ = 0), podczas gdy przy większych kątach pozorna powierzchnia emisji maleje proporcjonalnie do cos(θ). Ponieważ ciało doskonale czarne emituje promieniowanie równomiernie we wszystkich kierunkach, jego widmowa radiancja pozostaje stała, ale obserwowane natężenie zmienia się w zależności od efektów projekcji. Całkowitą moc emitowaną na jednostkę powierzchni można opisać, gdzie widmowa radiancja uwzględnia rzutowaną powierzchnię emisji.
\[\frac {d \Phi (dA, d \Theta, d \Omega, d \lambda)}{d \Omega} = B \lambda (T) \times dA \times d \lambda \times cos(\Theta)\]
W równaniu różniczkowy kąt bryłowy dΩ oznacza niewielką część kąta bryłowego, w którym promieniowanie jest emitowane lub mierzone. Opisuje on kierunkowość promieniowania i jest mierzony w steradianach sr. Różniczkowa powierzchnia dA oznacza nieskończenie mały obszar powierzchni emitującej. Reprezentuje ona niewielką część ciała doskonale czarnego lub dowolnej powierzchni promieniującej, która przyczynia się do emitowanego promieniowania. Różniczkowa szerokość pasma długości fali dλ odnosi się do małego przedziału widmowego w widmie emitowanego promieniowania.
Większość powierzchni nieprzewodzących można uznać za rozproszone lub „lambertowskie”. Oznacza to, że dla powierzchni lambertowskiej widmowa radiancja Bλ(T) i widmowa intensywność promieniowania Iλ(T) są liczbowo równe. Widmowa moc emisyjna M°(T) reprezentuje całkowitą moc emitowaną na jednostkę powierzchni ciała doskonale czarnego na jednostkę długości fali, zintegrowaną we wszystkich kierunkach półkuli.
\[I_\lambda=B_\lambda (T)=\frac {M°(T)}{\pi}\]
Jeśli chodzi o natężenie promieniowania I, wynika ono z równań, gdzie Iθ to natężenie promieniowania w [W/sr] z powierzchni widzianej pod kątem θ prostopadłym do powierzchni, a I0 to maksymalne natężenie emitowane w [W/sr] prostopadle do powierzchni.
\[I_\Theta= I_0 \times cos \Theta\]
Rysunek 1 poniżej ilustruje tę zależność dla ciała doskonale czarnego.
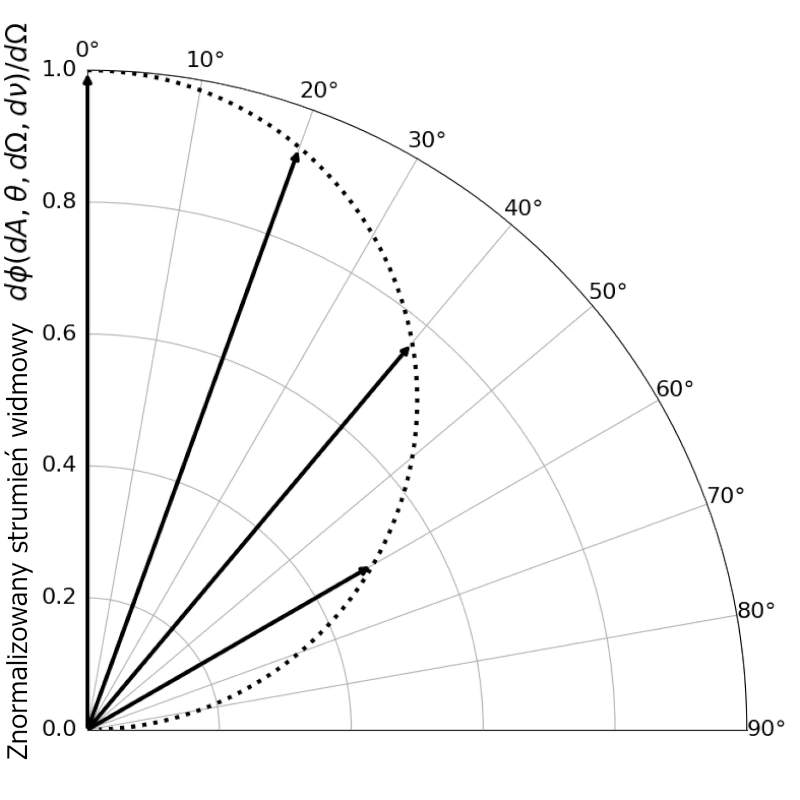
Rysunek 1: Większość powierzchni nieprzewodzących można uznać za rozproszone lub „lambertowskie”. Szybkość emisji w kierunku normalnym i nienormalnym dla obiektu dla powierzchni lambertowskiej. Ilość promieniowania skierowanego w dowolny klin jest proporcjonalna do powierzchni klina.
Reguła ta opiera się na teorii i obserwacjach empirycznych i zakłada, że powierzchnia nie jest lustrzana. Wraz ze wzrostem długości fali, dana powierzchnia materiału jest mniej prawdopodobna do uznania jej za lambertowską. Wynika to z faktu, że większość powierzchni jest uważana za „szorstką” w skali długości fali światła, jeśli materiał nie jest wypolerowany. Dlatego, gdy czujnik obserwuje powierzchnię pod kątem, natężenie promieniowania maleje proporcjonalnie do kosinusa kąta między obiektem docelowym a czujnikiem. Należy również zauważyć, że powierzchnie lustrzane nie podlegają tej regule, lecz prawu odbicia Snella dla optyki geometrycznej.
Podsumowanie
- Prawo Lamberta wyjaśnia, jak rozprzestrzenia się promieniowanie w zależności od powierzchni, kąta i długości fali, co jest pomocne w detekcji podczerwieni i obrazowaniu termicznym.
- Ciało doskonale czarne emituje promieniowanie we wszystkich kierunkach, ale wydaje się słabsze pod kątem ze względu na sposób rzutowania powierzchni.
Najwięcej promieniowania emitowane jest pionowo w górę (θ = 0), natomiast pod większymi kątami natężenie maleje.
Źródła
- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653
- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics rules of thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485
- De Witt, Nutter: Theory and Practice of Radiation Thermometry, 1988, John Wiley & Son, New York, https://doi.org/10.1002/9780470172575