Emisyjność w pomiarach w podczerwieni

Emisyjność to podstawowa właściwość w pomiarze temperatury w podczerwieni, która określa, jak efektywnie obiekt emituje promieniowanie podczerwone w porównaniu z idealnym ciałem czarnym. Wartość emisyjności określa zdolność materiału do emisji promieniowania cieplnego w porównaniu z idealnym ciałem czarnym, przyjmując wartości od 0 do 1. Emisyjność to rzeczywista energia promieniowania powierzchni, na którą wpływa temperatura i emisyjność zależna od materiału.

Ciało doskonale czarne to wyidealizowany obiekt, który pochłania całe padające promieniowanie bez odbicia ani transmisji i emituje maksymalną możliwą energię dla każdej długości fali. Jego rozkład promieniowania jest niezależny od kierunku. Jednak rzeczywiste materiały rzadko spełniają ten ideał. Ciała szare emitują znacznie mniej promieniowania w tej samej temperaturze. Materiał jest uważany za ciało „szare”, jeśli jego emisyjność pozostaje stała dla wszystkich długości fal, choć w naturze to nie występuje.

Emisyjność jest klasyfikowana na podstawie jej charakterystyki widmowej i kierunkowej:

• Całkowita emisyjność hemisferyczna ε: Scałkowana emisyjność w całym widmie.
• Emisyjność monochromatyczna ε_λ: Emisyjność przy określonej długości fali.
• Emisyjność półkulista ε_h: Emisyjność uśredniona we wszystkich kierunkach.
• Emisyjność kierunkowa ε_d: Emisyjność mierzona w określonym kierunku.

Z naukowego punktu widzenia, emisyjność półkulista εh to stosunek między promieniowaniem wyjściowym danej powierzchni M_λ(λ,T) a promieniowaniem wyjściowym M_λ°(λ,T) ciała doskonale czarnego o tej samej temperaturze i emisyjności ϵ=1. Emisyjność można określić dla określonej długości fali, kierunku i polaryzacji. [1]
\[\varepsilon_h(\lambda,T)=\frac{M_λ(\lambda,T)}{M°_\lambda (\lambda,T)}\]
Emisyjność półkulista jest wyznaczana poprzez całkowanie emisyjności kierunkowej po całej półkuli. Jego związek z normalną emisyjnością kierunkową jest regulowany przez współczynnik załamania światła, co umożliwia obliczenie jednej wartości na podstawie drugiej. To przybliżenie pozostaje aktualne nawet dla niegładkich powierzchni dielektrycznych, ponieważ chropowatość powierzchni ma minimalny wpływ na emisyjność. Podczas gdy powierzchnie dyfuzyjne wykazują wartości emisyjności kierunkowej podobne do ich półkulistych odpowiedników, powierzchnie zwierciadlane wykazują tendencję do spadku emisyjności przy większych kątach.

Emisyjność kierunkowa jest istotnym parametrem pomiaru temperatury w podczerwieni, ponieważ kamery termowizyjne i pirometry rejestrują promieniowanie cieplne z określonego kierunku, a nie ze wszystkich kątów. Urządzenia te zazwyczaj przyjmują wartości emisyjności padające prostopadle do powierzchni lub w jej pobliżu, co oznacza, że ​​pomiary wykonywane prostopadle do powierzchni zapewniają najdokładniejsze wyniki. Gdy pomiary muszą być wykonane pod kątem, może być konieczna korekta uwzględniająca zmiany emisyjności wraz z kątem obserwacji.

Prawo Kirchhoffa dotyczące promieniowania cieplnego stanowi, że dla ciała w równowadze termicznej emisyjność powierzchni jest równa jej absorpcji przy danej długości fali. Ponieważ całkowite promieniowanie padające na powierzchnię musi zostać wyemitowane, przepuszczone lub odbite, zależność tę wyraża poniższe równanie, gdzie τ to współczynnik przepuszczalności, a ρ to współczynnik odbicia na długość fali.
\[\varepsilon = 1 − \tau − \rho\]
W przypadku materiałów nieprzezroczystych o znacznej grubości, przez które światło nie przechodzi, emisyjność upraszcza się do następującego wzoru [2]:
\[\varepsilon = 1 − \rho\]
Podobnie jak inne właściwości optyczne, na emisyjność wpływa skład chemiczny i struktura geometryczna materiału. Można ją oszacować za pomocą parametrów optycznych, takich jak współczynnik załamania światła i współczynnik ekstynkcji. Współczynnik ekstynkcji reprezentuje tłumienie światła spowodowane rozpraszaniem i absorpcją na jednostkę objętości. Emisyjność jest regulowana równaniami opisującymi zachowanie dwóch odrębnych liniowych składowych polaryzacji. Te kierunki polaryzacji – spolaryzowany S (prostopadły do ​​płaszczyzny padania) i spolaryzowany P (równoległy do ​​niej) – definiują sposób oddziaływania fali padającej z powierzchnią. Każdy stan polaryzacji można rozłożyć na te ortogonalne składowe liniowe [1,3].

W dalszej części należy uwzględnić zespolony współczynnik załamania światła drugiego materiału, który wynosi n=n₂+ik, podczas gdy n₁ upraszcza się do 1. W poniższych równaniach obliczana jest moc emisyjna w zależności od kierunku polaryzacji. Wzory Fresnela mają zastosowanie tylko do gładkich powierzchni.
\[\varepsilon_p=1− \left( \frac{n \times cos(\phi)− \sqrt {1− \frac {sin^2(\phi)}{n^2}}}{n \times cos(\phi)+ \sqrt{1− \frac {sin^2(\phi)} {n^2} }} \right)^2\]
\[\varepsilon_s=1− \left( \frac{cos(\phi)−n \sqrt {1− \frac {sin^2(\phi)}{n^2}}}{cos(\phi)+n \sqrt{1− \frac {sin^2(\phi)} {n^2} }} \right)^2\]
PWiększość praktycznych zastosowań kładzie nacisk na niespolaryzowaną emisję w podczerwieni. Oznacza to równy rozkład mocy w polaryzacjach s i p, co oznacza, że ​​efektywna emisyjność materiału jest zasadniczo średnią z dwóch kierunków polaryzacji.
\[\varepsilon = \frac{1}{2}(\varepsilon_s + \varepsilon_p)\]
W przypadku emisji prostopadłej do powierzchni nie ma rozróżnienia między polaryzacją s i p. Zatem kierunkowa emisyjność normalna upraszcza się do następującego równania.
\[\varepsilon_n(ϕ=0°)=\frac{(4 n_1 n_2)}{(n_1+n_2)^2+k^2}\]
Ze względu na swoje wewnętrzne właściwości optyczne i fizyczne, każdy materiał wykazuje unikalne właściwości emisyjne dla różnych długości fal. W przypadku materiałów rzeczywistych emisyjność często zmienia się wraz z kątem emisji, co oznacza, że ​​nie zachowują się one jak powierzchnie lambertowskie (które emitują promieniowanie równomiernie we wszystkich kierunkach). Mimo to należy dokonać rozróżnienia między materiałami przewodzącymi a dielektrycznymi.

W przypadku materiałów dielektrycznych emisyjność maleje, gdy jest mierzona pod kątem ukośnym. Materiał dielektryczny to izolator elektryczny, który może magazynować i podtrzymywać pole elektrostatyczne, minimalizując jednocześnie straty energii. Rysunek 1 przedstawia przykładowo emisyjność kierunkową w funkcji kąta ekspozycji dla materiału dielektrycznego. Ten typowy kształt krzywej można również przenieść na materiały nieprzewodzące, takie jak szkło, tworzywa sztuczne lub materiały organiczne. Jedynym czynnikiem wpływającym na emisyjność gładkiego interfejsu dielektrycznego jest jego rzeczywisty współczynnik załamania światła. Można wywnioskować, że emisyjność jest stała do kątów 60°, a następnie spada zgodnie z prawem kosinusów Lamberta i dlatego może być uważana za lamberowską w tej dziedzinie.
Co więcej, rysunek 1 ilustruje przykładowo zależność między materiałem przewodzącym a materiałem przewodzącym. Co ciekawe, emisyjność kierunkowa materiałów przewodzących może wzrastać pod innymi kątami, a następnie spadać zgodnie z prawem kosinusów Lamberta. Mimo to emisyjność pozostaje niemal stała dla kątów do 60°, choć na niższym poziomie.

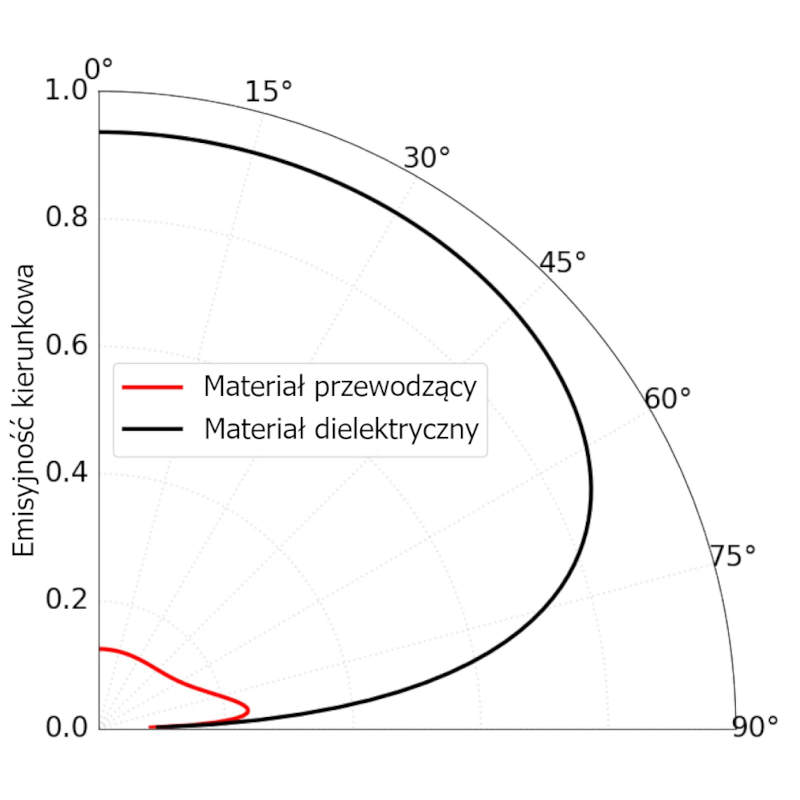
Rysunek 1: Przykładowa emisyjność kierunkowa jako funkcja kąta emisji dla materiału dielektrycznego (czarna krzywa) o współczynniku załamania n = 1,7 i materiału przewodzącego (czerwona krzywa) o n = 2,8 i k = 4,4. Materiał dielektryczny wykazuje wysoką emisyjność pod wszystkimi kątami, stopniowo malejąc przy kątach ukośnych. Natomiast materiał przewodzący wykazuje bardzo niską emisyjność, która ulega dalszemu zmniejszeniu przy większych kątach ze względu na wysoki współczynnik odbicia. Podkreśla to silną zależność kątową emisyjności dla różnych typów materiałów.

Emisyjność zależy od kierunku i zmienia się w zależności od długości fali – właściwość ta znana jest jako emisyjność widmowa. Ta zmienność występuje, ponieważ materiały w różny sposób oddziałują z promieniowaniem podczerwonym przy różnych długościach fali ze względu na swoją strukturę atomową i molekularną. Absorpcja i emisja promieniowania cieplnego są regulowane przez przejścia elektronowe, mody drgań i oddziaływania sieci krystalicznej, które zależą od długości fali. Ze względu na wysoki współczynnik odbicia, przewodniki, takie jak metal, mają tendencję do niższej emisyjności przy dłuższych długościach fal podczerwonych. Z kolei dielektryki, takie jak ceramika lub tlenki, wykazują wyższą emisyjność w określonych pasmach widmowych, w których ich drgania molekularne silnie absorbują i reemitują energię. Jak widać na rysunku 2, zależność ta jest szczególnie istotna w pomiarach temperatury w podczerwieni, ponieważ wybór odpowiedniego zakresu widmowego zapewnia dokładne odczyty, zwłaszcza w przypadku materiałów o zmiennej emisyjności w całym spektrum podczerwieni.

 
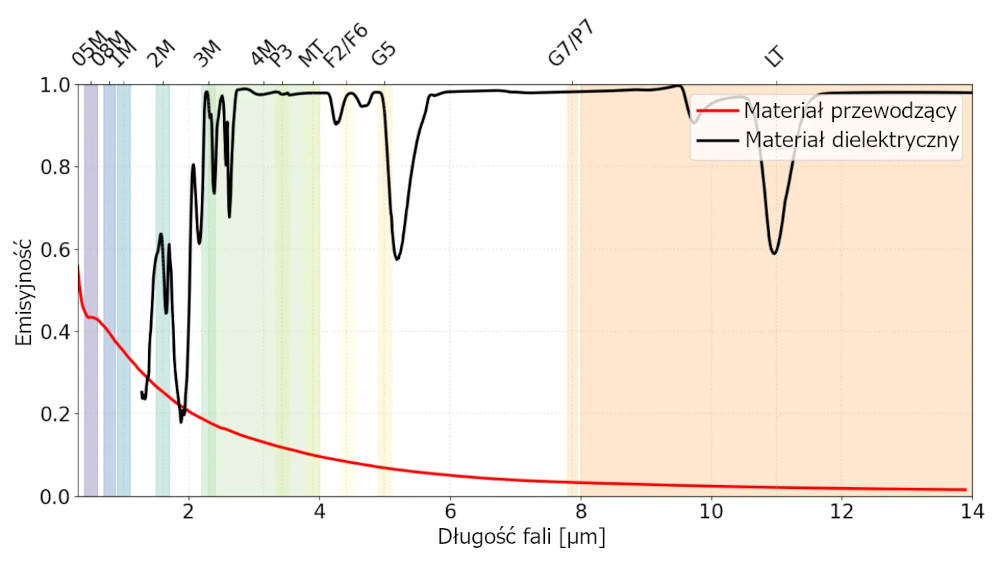
Rysunek 2: Przykładowa emisyjność kierunkowa w funkcji długości fali dla przewodnika (czerwona krzywa) i materiału dielektrycznego (czarna krzywa) pod kątem prostym. Przewodnik wykazuje niską emisyjność we wszystkich długościach fal, ze stopniowym spadkiem wraz ze wzrostem długości fali, co jest charakterystyczne dla powierzchni metalowych o wysokim współczynniku odbicia. Natomiast materiał dielektryczny wykazuje wysoką emisyjność w większości obszarów podczerwieni, z wyjątkiem określonych zakresów długości fal, w których występują efekty transmisji lub odbicia.

Gdy powierzchnia materiału jest chropowata, jego emisyjność wzrasta z powodu wielokrotnych odbić i rozpraszania promieniowania cieplnego w mikrostrukturach chropowatej powierzchni. Chropowatość ma duży wpływ na metale o niskiej emisyjności, ale relatywnie mniejszy wpływ na dielektryki o wysokiej emisyjności. Gładka powierzchnia odbija więcej promieniowania padającego, zmniejszając ilość pochłanianego i emitowanego. Natomiast chropowata powierzchnia tworzy liczne mikroskopijne wnęki, które zatrzymują promieniowanie, zwiększając absorpcję i reemisję. Efekt ten jest szczególnie wyraźny w metalach, gdzie polerowane powierzchnie mają niską emisyjność ze względu na wysoki współczynnik odbicia. Wraz ze wzrostem chropowatości, efektywna powierzchnia emisji rośnie, umożliwiając wypromieniowanie większej ilości energii. Dodatkowo, nierówności powierzchni zakłócają odbicie zwierciadlane, przekształcając je w odbicie rozproszone, co zwiększa absorpcję energii i zmniejsza straty spowodowane odbiciami zewnętrznymi. W skali mikroskopowej chropowate powierzchnie mogą również zmieniać właściwości optyczne materiału, wpływając na jego interakcję z promieniowaniem podczerwonym. To połączenie zwiększonej absorpcji, wielokrotnych wewnętrznych odbić i zwiększonej powierzchni skutkuje wyższą całkowitą emisyjnością. Poniższe równanie przedstawia zależność między chropowatością R_a, która określa ilościowo odchylenie profilu powierzchni od linii średniej, a emisyjnością widmową między dwoma stanami powierzchni z tym samym materiałem [4, 5, 6].

\[\varepsilon = \left( 1 + (\frac {1}{\varepsilon_0} − 1) \frac{R_a}{R_0} \right) ^{−1}\]

W równaniu ε0 oznacza emisyjność gładkiej powierzchni, a R₀ odnosi się do początkowej chropowatości. Równanie to wyraża asymptotyczny wzrost emisyjności wraz ze wzrostem chropowatości. Chropowatość powierzchni zmienia się w zależności od obróbki – metale polerowane na wysoki połysk mają chropowatość 0,01–0,1 µm, metale obrabiane mechanicznie 0,1–5 µm, a powierzchnie śrutowane osiągają chropowatość 5–50 µm. Powierzchnie powlekane lub utleniane mają chropowatość od 0,5 do 10 µm, podczas gdy metale odlewane lub skorodowane zazwyczaj przekraczają 50 µm.

 
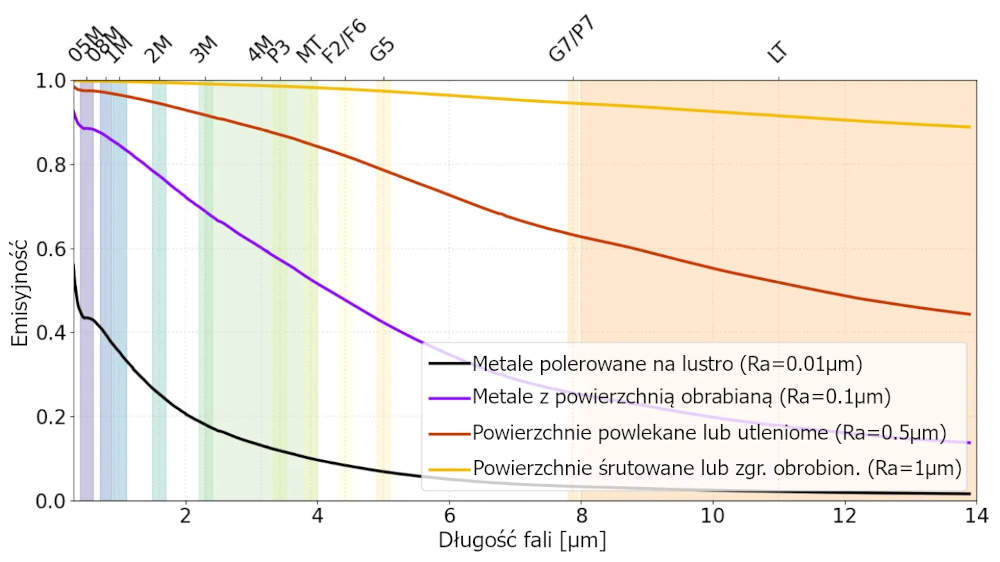
Rysunek 3: Przykładowa emisyjność w funkcji długości fali dla powierzchni metalowych o różnym stopniu chropowatości. Wykres porównuje cztery stany powierzchni: metale polerowane na wysoki połysk, powierzchnie obrabiane mechanicznie, powierzchnie powlekane lub utleniane oraz powierzchnie śrutowane lub chropowate.

Emisyjność jest również zależna od temperatury, ponieważ wewnętrzne właściwości optyczne materiału mogą zmieniać się pod wpływem wzbudzenia termicznego. W wyższych temperaturach zmiany gęstości elektronowej, drgania sieci krystalicznej i przemiany fazowe wpływają na zdolność materiału do emisji promieniowania cieplnego. W metalach wzrost temperatury może prowadzić do wzrostu rozpraszania swobodnych elektronów, co może zwiększać emisyjność przy określonych długościach fal. Dielektryki i materiały ceramiczne często wykazują zwiększoną emisyjność w podwyższonych temperaturach ze względu na zwiększoną aktywność fononów i zmiany absorpcji przerwy energetycznej. Ponadto utlenianie powierzchni lub przemiany strukturalne w wysokich temperaturach mogą modyfikować emisyjność poprzez zmianę współczynnika odbicia i absorpcji materiału. Rysunek 4 przedstawia zmiany całkowitej emisyjności dla znanych materiałów, których emisyjność zmienia się wraz z temperaturą.

 
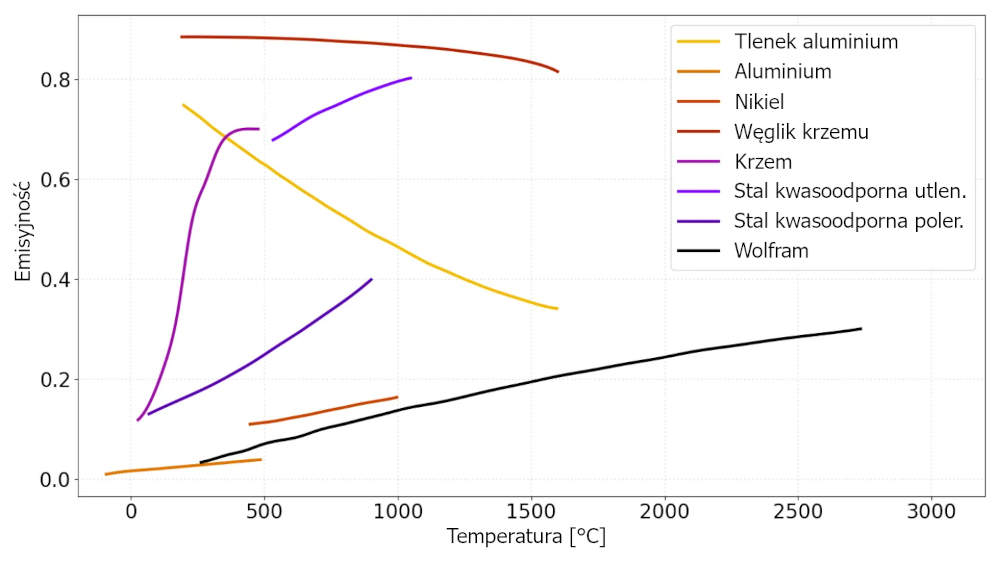
Rysunek 4: Całkowita emisyjność w funkcji temperatury dla różnych materiałów, w tym metali, tlenków i ceramiki. Metale takie jak wolfram (czarna krzywa), aluminium (pomarańczowa krzywa) i nikiel (ciemnopomarańczowa krzywa) wykazują niską emisyjność, która stopniowo rośnie w wyższych temperaturach. Polerowana stal nierdzewna (ciemnofioletowa krzywa) również wykazuje niską emisyjność, podczas gdy jej utleniona forma (jasnofioletowa krzywa) ma znacznie wyższą emisyjność. Materiały niemetaliczne, takie jak węglik krzemu (czerwona krzywa) i tlenek glinu (żółta krzywa), utrzymują wysoką emisyjność w całym zakresie temperatur.

Gdy materiał jest półprzezroczysty, na jego emisyjność wpływają zarówno jego właściwości optyczne, jak i grubość, ze względu na częściową transmisję i wewnętrzne odbicia promieniowania podczerwonego. W bardzo cienkich warstwach znaczna część promieniowania może przejść przez materiał, zmniejszając jego efektywną emisyjność. Wraz ze wzrostem grubości, absorpcja staje się bardziej dominująca, co prowadzi do wyższych wartości emisyjności. Mogą jednak również wystąpić efekty interferencyjne, w których określone długości fal ulegają konstruktywnej lub destruktywnej interferencji w warstwie, co dodatkowo zmienia emisyjność w sposób zależny od długości fali. Rysunek 5 ilustruje to zachowanie dla cienkiej folii z tworzywa sztucznego, pokazując, jak zmiany grubości wpływają na zdolność materiału do emisji promieniowania podczerwonego.

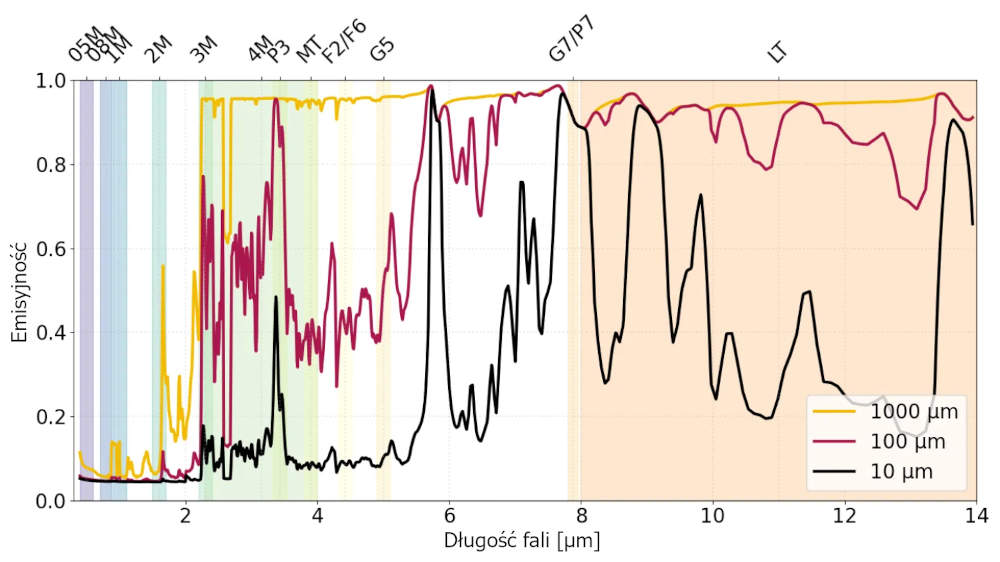
Rysunek 5: Emisyjność jako funkcja długości fali dla folii z politereftalanu etylenu (PET) o różnej grubości (10 µm, 100 µm i 1000 µm). Dane ilustrują, jak emisyjność zależy zarówno od długości fali, jak i grubości materiału. Cieńsze folie (10 µm, czarna krzywa) wykazują niższą emisyjność i silne wahania zależne od długości fali ze względu na częściową przezroczystość i efekty interferencji. Wraz ze wzrostem grubości emisyjność generalnie rośnie, przy czym folia o grubości 1000 µm (żółta krzywa) zbliża się do nieprzezroczystego zachowania z wysoką i stabilną emisyjnością w większości długości fal.

Podsumowanie

• Emisyjność okresala, jak efektywnie materiał emituje promieniowanie podczerwone w porównaniu z ciałem doskonale czarnym (wartość od 0 do 1).
• Rodzaje emisyjności: całkowita (wszystkie długości fal), monochromatyczna (określona długość fali), półkulista (wszystkie kierunki) i kierunkowa (określony kąt).
• Rzeczywiste materiały nie są ciałami doskonale czarnymi; Mogą to być ciała szare (stała emisyjność) lub zmieniać się w zależności od długości fali i kierunku.
• Czynnikami wpływającymi mogą być:
  • Skład materiału (metale mają niską emisyjność, dielektryki mają wyższą emisyjność).
  • Chropowatość powierzchni zwiększa emisyjność poprzez zmniejszenie współczynnika odbicia.
  • Temperatura wpływa na emisyjność ze względu na zmiany właściwości optycznych niektórych materiałów.
  • Grubość wpływa na emisyjność w materiałach półprzezroczystych i cienkich materiałach ze względu na efekty transmisji i interferencji.
  • Kąt patrzenia wpływa na emisyjność, szczególnie w przypadku powierzchni odblaskowych.

Źródła

1. Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653
2. Salisbury, J. W., A. Wald, and D. M. D’Aria (1994), Thermal-infrared remote sensing and Kirchhoff’s law: 1. Laboratory measurements, Geophys. Res., 99(B6), 11897–11911, https://doi.org/10.1029/93JB03600.
3. Warren, T. J., Bowles, N. E., Donaldson Hanna, K., & Bandfield, J. L. (2019). Modeling the angular dependence of emissivity of randomly rough surfaces. Journal of Geophysical Research: Planets, 124, 585–601. https://doi.org/10.1029/2018JE005840
4. Zhang, Z., Chen, M., Zhang, L. et al. A straightforward spectral emissivity estimating method based on constructing random rough surfaces. Light Sci Appl 12, 266 (2023). https://doi.org/10.1038/s41377-023-01312-1
5. Chang-Da Wen, Issam Mudawar, Modeling the effects of surface roughness on the emissivity of aluminum alloys, International Journal of Heat and Mass Transfer, Volume 49, Issues 23–24, 2006, Pages 4279-4289, ISSN 0017-9310, https://doi.org/10.1016/j.ijheatmasstransfer.2006.04.037
6. Agababov, S. G. (1968). Effect of the roughness of the surface of a solid body on its radiation properties and methods for their experimental determination. High Temperature, 6, 76-85.