Promieniowanie podczerwone i temperatura
Wszystkie obiekty emitują promieniowanie podczerwone o temperaturze powyżej zera absolutnego. Wraz ze wzrostem temperatury obiektu wzrasta natężenie emitowanej energii, co umożliwia pomiar temperatury poprzez analizę promieniowania podczerwonego. Prawo promieniowania Plancka ustanawia fundamentalną zasadę bezkontaktowego pomiaru temperatury, wykazując, że wszystkie obiekty o temperaturze wyższej niż zero absolutne (-273,15°C lub 0 K) emitują promieniowanie elektromagnetyczne. W przypadku ciała doskonale czarnego – idealnego obiektu, który pochłania i emituje promieniowanie o wszystkich długościach fal – natężenie emisji promieniowania podczerwonego rośnie wraz z temperaturą, co umożliwia określenie temperatury na podstawie emitowanej energii podczerwonej. Prawo promieniowania Plancka wskazuje również, że im wyższa temperatura ciała, tym więcej promieniowania emituje ono wykładniczo we wszystkich długościach fal. Widmowa wartość promieniowania na jednostkę powierzchni, na jednostkę kąta bryłowego i na jednostkę częstotliwości dla danej długości fali promieniowania jest opisana w prawie Plancka, gdzie c to prędkość światła, h to stała Plancka, a k to stała Boltzmanna [1, 2, 3].
\[B_\lambda(\lambda, T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda kT}} - 1} \]
Prawo Plancka występuje w kilku postaciach i można je również zapisać za pomocą gęstości widmowej energii \(u_\lambda(\lambda,T)\):
\[u_{\lambda} (\lambda,T) = \frac {4 \pi}{c}B_\lambda (\lambda,T)\]
W powyższych wariantach prawa Plancka należy używać terminów 2hc2 i hc/kB, które obejmują jedynie stałe fizyczne. W związku z tym terminy te można traktować jako stałe fizyczne i dlatego określa się je jako pierwszą stałą promieniowania c1 = 3,74 ∙10−16 W/m2 i drugą stałą promieniowania c2 = 1,44 ∙10−2 K/m. W prawie Plancka, Bλ(λ,T) i M°λ(λ,T) opisują różne aspekty promieniowania ciała doskonale czarnego. Natomiast Bλ(λ,T), znane jako radiancja widmowa, reprezentuje natężenie promieniowania emitowanego na jednostkę długości fali i jednostkę kąta bryłowego. Jest mierzona w Wm−2μm−1sr−1, co oznacza, że określa ona ilościowo promieniowanie w określonym kierunku. Natomiast [Równanie], widmowa moc emisyjna opisuje całkowitą moc emitowaną na jednostkę powierzchni i na jednostkę długości fali, całkując po wszystkich kierunkach. Jej jednostką jest Wm−2μm−1. Poniższe równanie wiąże te dwie wielkości.
\[M°_\lambda (λ,T)=\pi B_\lambda (\lambda,T)\]
Dlatego prawo Plancka można przeformułować na widmową radiancję wyjściową [równanie] ciała doskonale czarnego w półprzestrzeń w zależności od jego temperatury i długości fali [1,2,3].
\[M°\lambda (\lambda,T)= \frac{c_1}{λ^5} \frac{1}{e^\frac{c_2}{\lambda T}−1}\]
Te wzory są bardzo abstrakcyjne, dlatego nie można ich wykorzystać w wielu praktycznych zastosowaniach. Wynika z nich jednak wiele obserwacji fizycznych. Emitowana energia podczerwieni rośnie wraz z temperaturą obiektu, a szczytowa długość fali przesuwa się w kierunku krótszych fal. Wraz ze wzrostem temperatury, maksimum promieniowania spektralnego przesuwa się w kierunku krótszych fal. W wyższych temperaturach ilość promieniowania podczerwonego wzrasta i jest odczuwalna jako ciepło, a emitowane jest więcej promieniowania widzialnego, przez co ciało świeci na czerwono. W wyższych temperaturach ciało jest jasnożółte lub niebiesko-białe i emituje znaczne ilości promieniowania krótkofalowego.
W temperaturze pokojowej (~300 K) ciało emituje promieniowanie cieplne, głównie w podczerwieni, które jest niewidzialne. Jego szczyt przypada na około 10…14 µm, dlatego większość kamer termowizyjnych pracuje w tym zakresie widmowym do pomiaru temperatury. Niemniej jednak, promieniowanie Plancka mówi, że im wyższa temperatura ciała, tym więcej promieniowania emituje ono dla każdej długości fali.
Moc emitowana z powierzchni emitującej, na jednostkę rzutowanej powierzchni emitującej, na jednostkę kąta bryłowego, na jednostkę długości fali. Ponieważ radiancja jest izotropowa i niezależna od kierunku, moc emitowana pod kątem do normalnej jest proporcjonalna do rzutowanej powierzchni, a zatem do kosinusa tego kąta, zgodnie z prawem kosinusów Lamberta, i jest niespolaryzowana.
Poniższa ilustracja, przedstawia graficzny opis wzoru w zależności od długości fali przy różnych temperaturach.
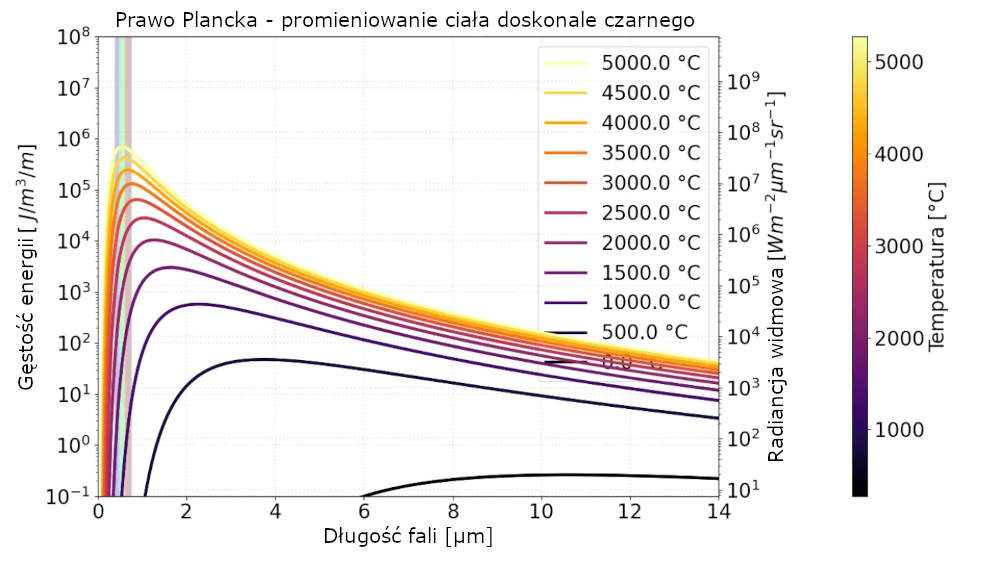
Rysunek 1: Natężenie promieniowania podczerwonego rośnie wykładniczo wraz z temperaturą i przesuwa się w kierunku krótszych fal.
Odwrócenie równania 1 daje temperaturę ciała czarnego dla danej intensywności widmowej przy długości fali wąskopasmowej, która jest następująca:
\[T=\frac {hc}{\lambda \times k_B \times ln(\frac{2hc^2}{λ^5 B_\lambda}+1)}\]
Podsumowanie
- Każdy obiekt o temperaturze powyżej zera absolutnego (-273.15°C lub 0 K) emituje promieniowanie podczerwone.
- Gdy temperatura rośnieni, ilośćemitowanego promieniowania wrasta wykładniczo dla każdej długości fali.
- Ciało doskonale czarne (idelany emiter) emituje więcj promieniwania gdy jego temperatura wzrasta.
- W temperaturze pokojowej (~300 K), większość emitowanego promieniowania przypada na zakres 10…14 µm, dlatego większość kame temowizyjnych pracuje w tym paśmie.
Źródła
- Hecht, Eugene. Optik, Berlin, Boston: De Gruyter, 2018. https://doi.org/10.1515/9783110526653
- Miller, J. L., Friedman, E., Sanders-Reed, J. N., Schwertz, K., & McComas, B. (2020). Photonics rules of thumb (No. PUBDB-2021-03249). Bellingham, Washington: SPIE Press. https://doi.org/10.1117/3.2553485
- De Witt, Nutter: Theory and Practice of Radiation Thermometry, 1988, John Wiley & Son, New York, https://doi.org/10.1002/9780470172575